Эксперимент с тремя телами
Физическая модель
Одним из примеров хаотической системы является движение трех тел, для простоты - 2 тела фиксированы, а вокруг них вращается третье. Физическая модель - обычное гравитационное взаимодействие, т.е.:

G - берется обычной константой, которая настраивается в программе. Далее в дискретной модели на каждом шаге рассчитывается результирующая сила, действующая на тело:

Где:

m - масса тела, для которого производится расчет, M1 и M2 - тела вокруг которых идет вращение, R1 и R2 - расстояние соответственно между m и M1, m и M2. Далее результирующее ускорение тела становится:

И уже исходя из этого считается перемещение за один дискретный шаг работы (интегрируется):
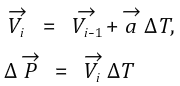
Тем самым получается изменение позиции. Точка рисуется на новой позиции и производится новый рассчет. Алгоритм очень примитивен, то же интегрирование идет банальными прямоугольниками, хотя лучше использовать что-то более сложное (хотя бы полиномы Адамса).
Работа демонстрации
Ниже идут скриншоты работы демонстрации. Порой получаются очень красивые картины.
Пример апериодических колебаний. В конце концов тело ушло в бесконечность. Это результат неточности физической модели: она некорректно отрабатывает слишком сильные сближения тел и возникающие при этом высокие скорости. В реальном мире (соответственно сами тела не точки, а объекты с физ. размерами) скорее всего произойдет столкновение тел.

Вот здесь колебания продлились куда дольше:

Периодически появляются стабильные системы. В основном они лежат при достаточно большом удалении траектории тела от центра масс системы.

Еще один стабильный пример, если подождать достаточно долго, он в итоге должен превратиться в подобие предыдущего рисунка:

Ссылки
Исходный текст демонстрации представлен в файле: 3body.zip Демонстрация легко расширяется до произвольного количества тел. При желании можно установить в ней параметры Солнечной системы и увидеть, что она более-менее стабильно будет крутиться. После хаотических картин, наблюдаемых выше, это будет удивлять, сколько же было ошибок и катастроф на этапе формирования нашей солнечной системы и насколько сложным был этот процесс.